Ensemble des séquences typiques \(\mathcal T_\varepsilon^{(n)}\)
Ensemble de séquences dont la probabilité d'apparition est une grande partie de la probabilité totale. $$\begin{align}\mathcal T_\varepsilon^{(n)}&=\{x_{1:n}\in\mathcal X^n\mid 2^{-n(H(X)+\varepsilon)}\leqslant p(x_{1:n})\leqslant2^{-n(H(X)-\varepsilon)}\}\\ &=\{x_{1:n}\in\mathcal X^n\mid H(X)-\varepsilon\leqslant-\log_2(p(x_{1:n}))/n\leqslant H(X)+\varepsilon\}\end{align}$$

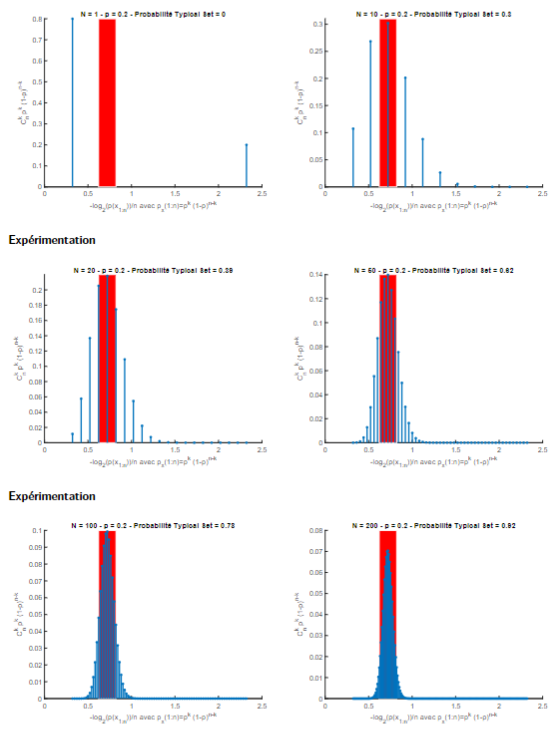
• \({\Bbb P}(x_{1:n}\in\mathcal T^{(n)}_\varepsilon)\) \(\gt 1-\varepsilon^\prime\) lorsque \(n\to+\infty\)
• \((1-\varepsilon^\prime)2^{n(H(X)-\varepsilon)}\) \(\leqslant\lvert\mathcal T_\varepsilon^{(n)}\rvert\leqslant\) \(2^{n(H(X)+\varepsilon)}\)
    
• on a \(\lvert\mathcal T_\varepsilon^{(n)}\rvert\approx\) \(2^{nH(X)}\), et la probabilité d'apparition de chaque séquence typique est \(\approx\) \(2^{-nH(X)}\)
• intérêt : les propriétés statistiques de la source tendent à favoriser l'apparition de séquences typiques, pour lesquelles il va falloir un traitement spécifique lors du codage source

Questions de cours

Montrer que $$\lvert\mathcal T_\varepsilon^{(n)}\rvert\leqslant2^{n(H(X)+\varepsilon)}$$

Minorer la probabilité de l'ensemble des séquences par la probabilité des séquences typiques.

Majorer par la borne de probabilité des séquences typiques.

La probabilité ne dépend plus de \(x_{

n}\) : on peut faire apparaître le cardinal.

Montrer que $$(1-\varepsilon^\prime)2^{n(H(X)-\varepsilon)}\leqslant\lvert\mathcal T_\varepsilon^{(n)}\rvert$$

Utiliser la majoration d'appartenance à \(\mathcal T_\varepsilon^{(n)}\).

Majorer par la borne de probabilité de l'ensemble \(\mathcal T_\varepsilon^{(n)}\).

La probabilité ne dépend plus de \(x_{

n}\) : on peut faire apparaître le cardinal de \(\mathcal T_\varepsilon^{(n)}\).

'information